Mathematical Mechanism Behind the Rugged Structures at Cell Boundaries

The mathematical and biological mechanisms underlying the rugged structures at cell boundaries present in tissues like the kidneys and nasal glands have been discovered. The researchers expect that their new findings may aid in the development of new treatments for associated pathologies as well as the development of better biological models for future research.

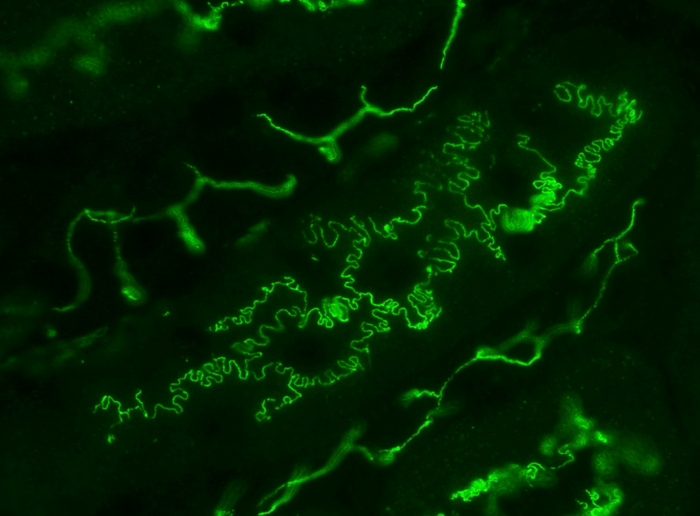
Photo of mouse renal tubules in vivo, immunostained for plasma membrane protein occludin (green). Many epithelial cells like the ones shown here have rugged boundaries described as interdigitated. It is proposed that interdigitation facilitates the transport of molecules and fluid between cell boundaries. Image Credit: Kyushu University/Miura Lab

Human cells come in a variety of sizes and forms. The form and structure of a cell are essential to its function in the body, from the neurons that spread across the central nervous system to the spherical white blood cells that protect us from infection. The structures between cells can also differ and are important.

The “rugged” or “wavey” pattern typically observed between epithelial cells, the type of cell that protects the skin and most other organs and blood vessels is one such in-between structure. These patterns may appear disorderly under a microscope, but Professor Takashi Miura of Kyushu University’s Faculty of Medical Sciences finds them fascinating.

It almost looks like the interlocking teeth on a zipper. Researchers also describe these structures as interdigitated cell boundaries. Many cells have interdigitated cell boundaries. For example, kidney podocytes that work as filters to generate urine have very intricated interdigitation patterns. Plant leaf epidermal cells look like a jigsaw puzzle so as to reduce the mechanical stress on cell walls.”

Takashi Miura, Professor, Faculty of Medical Sciences, Kyushu University

Takashi Miura led the research. The research was published in iScience.

One important role of epithelial cells is to enable the movement of molecules and fluids across cell borders, a process known as paracellular transport. Recent research suggests that interdigitating the border improves transit efficiency. However, how these structures originate and their physiological importance is still unknown.

We began by studying the interdigitation in MDCK cells, a type of epithelial cell originally from kidneys and commonly used in studying epithelial pattern formation. We found something unexpected when we mathematically broke down the cell-cell boundary pattern. It turns out that these seemingly random structures are not random at all, and in fact are mathematically scaling. In other words, the pattern has self-similarity—if you magnified the boundary, it holds the same characteristics as the original pattern.”

Takashi Miura, Professor, Faculty of Medical Sciences, Kyushu University

The researchers then delved into proven mathematical models to figure out how and why the interdigitation patterns take this definite form. After testing a number of theories, they settled on the Edwards-Wilkinson model.

The Edwards-Wilkinson model is used to mathematically simulate a randomly shaking boundary with a function of minimizing the length of that boundary. The scaling of cell boundaries we found fits into this model. After this, our next step was to find the molecular mechanism responsible for these dynamics.”

Takashi Miura, Professor, Faculty of Medical Sciences, Kyushu University

The researchers concentrated on the role of actomyosin, the actin-myosin protein complex that is responsible for practically all cellular actions that need force. They discovered certain myosin proteins that would reside on the bending cell border after careful observation.

Miura notes that their new findings improve their grasp of cell dynamics principles and contribute to the greater trend of establishing the mathematical basis of biology.

Takashi Miura adds, “Mathematics has always been inextricably linked in the fields of Chemistry and Physics. Mathematically breaking down fundamental processes in Biology is still a relatively new domain that has grown markedly over the last 20 years. I think it shows that the field of Biology is maturing. As we develop this field, it will give us new perspectives on the fundamentals of life, and the beauty of biological patterns.”